TEOREMA DE LA PROBABILIDAD TOTAL

Sea A1,A2,…,An un sistema completo de sucesos y B un suceso cualquiera asociado al mismo experimento. Entonces, se cumple que:

P(B)=P(A1)⋅P(B/A1)+P(A2)⋅P(B/A2)+…+P(An)⋅P(B/An)

Tenemos tres cajas con bombillas. La primera contiene 10 bombillas, de las cuales hay cuatro fundidas; en la segunda hay seis bombillas, y tan sólo una fundida, y en la tercera hay tres bombillas fundidas de un total de ocho. ¿Cuál es la probabilidad de que si escogemos una caja al azar, y cogemos una bombilla, ésta esté fundida?

Escribiremos C1, C2, C3 si escogemos las cajas 1, 2, y 3, respectivamente.

Como la elección es al azar, tenemos probabilidad 1 de escoger cada caja.

                                                                        3

El suceso que nos interesa es F= "bombilla fundida", por lo que  F = "bombilla no fundida".

Lo representamos en un diagrama en árbol:

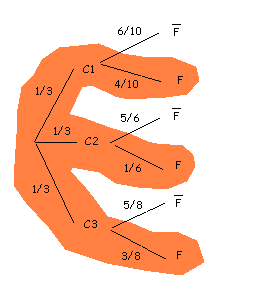
Están marcadas en naranja las tres ramas que nos interesan, las que acaban en "bombilla fundida".

(C1,C2,C3) es un sistema completo de sucesos, ya que siempre escogeremos una de las tres cajas (es decir, su unión es el total), y no podemos escoger más de una (es decir, son incompatibles dos a dos).

Aplicamos, pues, el teorema de la probabilidad total:

P(F)=P(C1)⋅P(F/C1)+P(C2)⋅P(F/C2)+P(C3)⋅P(F/C3)

= 1 . 4 + 1 . 1 + 1 . 3 = 4 + 1 + 3 = 113

     3  10   3   6     3   8   30   18   24   360

Como vemos, aplicar el teorema de la probabilidad total no es otra cosa que calcular la probabilidad mediante un diagrama de árbol.

Lo único con lo que tenemos que ir con cuidado es a la hora de calcular las probabilidades de cada rama.