TEOREMA DE BAYES
El teorema de Bayes es utilizado para calcular la probabilidad de un suceso, teniendo información de antemano sobre ese suceso.
Podemos calcular la probabilidad de un suceso A, sabiendo además que ese A cumple cierta característica que condiciona su probabilidad. El teorema de Bayes entiende la probabilidad de forma inversa al teorema de la probabilidad total. El teorema de la probabilidad total hace inferencia sobre un suceso B, a partir de los resultados de los sucesos A. Por su parte, Bayes calcula la probabilidad de A condicionado a B.
Para calcular la probabilidad tal como la definió Bayes en este tipo de sucesos, necesitamos una fórmula. La fórmula se define matemáticamente como:
Donde B es el suceso sobre el que tenemos información previa y A(n) son los distintos sucesos condicionados. En la parte del numerador tenemos la probabilidad condicionada, y en la parte de abajo la probabilidad total. En cualquier caso, aunque la fórmula parezca un poco abstracta, es muy sencilla. Para demostrarlo, utilizaremos un ejemplo en el que en lugar de A(1), A(2) y A(3), utilizaremos directamente A, B y C.
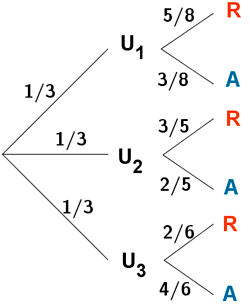
EJEMPLO: Tenemos tres urnas distintas: U1 con 5 bolas rojas y 3 azules, U2 con 3 bolas rojas y 2 azules y U3 con 2 bolas rojas y 4 azules. Escogemos una urna al azar y extraemos una bola. Si la bola ha sido azul, ¿cuál es la probabilidad de que haya sido extraida de la urna U2?
Sean los sucesos R = {Sacar bola roja} y A = {Sacar bola azul}. En el diagrama de árbol podemos ver las distintas probabilidades de que ocurran R o A para cada una de las 3 urnas.
La probabilidad pedida es P(U2/A). Utilizando la regla de Bayes, tenemos:
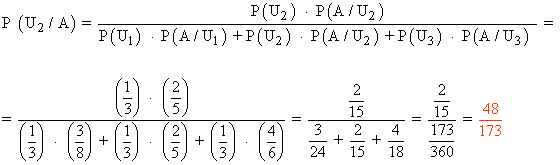

No hay comentarios:
Publicar un comentario